Ekok Çiftleri
Pruva Akademi 8. Sınıf Matematik Sorular Konuşuyor, Çarpanlar ve Katlar, Test 2
Uyarı!
Bu sorularda 1 sayısının sayılıp sayılmadığına dikkat etmeniz gerek, eğer soru soruyorsa her çıkan sonuç için bir eklememiz gerek.
Okumak istemeyenler için formül (herkes anlamayabilir)
Sorudaki üst limit n iken (yukarıdaki soruda 12):
$$ \mathbb{P} = \{p \in \N \mid p \text{ asal}\} $$ $$ \sum_{i = 2}^{n} \frac{(\prod_{p \in \mathbb{P}} 2v_p(i) + 1) - 3}{2} $$
Çözüm
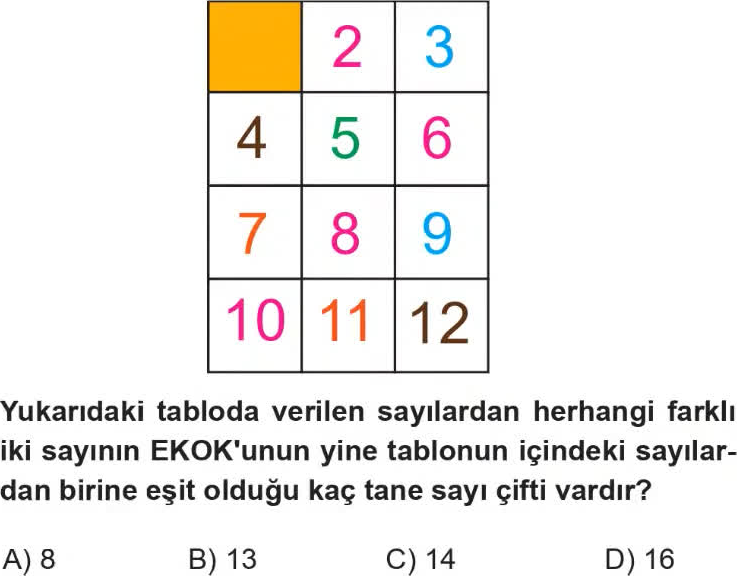
Bu tip soruları çözmek için bu sayıdan küçük olan tüm sayıları düşünmemiz gerektirdiği için biraz yorucu bir soru tipi, fakat kolaylaştırılabilir. 1 dahil olmadığından 2 ile başlıyoruz: Tek bir sayı ile bir şey yapamayız çünkü sayıların farklı olmasını istemiş bu sebeble 3’e geçtiğimizde de sonuç benzer, fakat 4’e geçtiğimizde şunu yazabiliriz. $$ EKOK(a, b) = 2^2 $$ a da b de \(2^2\)’nin katı olmak zorunda, bu durumda hem a hem de be için 3 olasılığımız var yani toplamda \(3^2\) olasılığımız oluyor, fakat bu sayıdan hem a’nın da b’nin de \(2^2\)’nin katı olmadığı seferleri çıkarmamız gerek, bu ise her ikisi de \(2^1\)‘in katı olduğunda olur yani toplamda \(2^2\) durum çıkarılmalı. Bu bize \(9-4\) yani 5’i verir, fakat bu doğru eklememiz gereken sayı değil, çünkü bu sayıyı düzenliden düzensize çevirmemiz gerek. Bunu yapmak için şunu bilmemiz gerek her ikisinin de 4 olduğu sefer dışında her sefer iki kere saydık bu yüzden $$ (5+1)/2 = 3 $$ işlemi ile bunu sıralıya çevirmemiz gerek, fakat okularım bunun da eksik olduğunu fark edecekler, bunun nedeni ikisinin de 4 olduğu ve içinde 1 olan durumlardır, bunları çıkardığımızda $$ 3 - 2 = 1 $$ buluyoruz. Bunu asal sayılar dışında 12’den küçük her sayı ile yapmamız gerekiyor, işte burada fark ediyoruz bunun neden uzun süreceğini, asal sayıları çıkardığımızdabunu 5 sayı için yapmamız gerekiyor ve bizim asal çarpanlara ayırmada çok iyi olmamızı gerektiriyor. Ayrıca bazıları şimdiden peki bunu 6 veya 10 için nasıl uygularım diye düşünecek, bunun için farklı asal çarpanlarını düşünmemiz gerekecek. Örneğim 12 sayısını ele alalım: $$ 12 = 2^2 \cdot 3^1 $$ \(2^2\) kısmını daha önce 4 için hesaplamıştık, ama bu sefer tekrar edeni ve içinde 1 olanı sonradan çıkarmamız gerek o yüzden çıkardığımız ikiyi yerine koyuyoruz: $$ 1 + 2 = 3 $$ Ve sonra tekrar iki ile çarpıyoruz. $$ 3 \cdot 2 = 6 $$ Ve eklediğimiz biri de geri alıyoruz $$ 6 - 1 = 5 $$ Şimdi ise 3 için hesaplayacağız, bunun için de asal sayılarda 0 artırdığımız için 0’a 2 ekleyerek 2 bulacağız ve çarparak 4 bulup 1 çıkaracağız, 3 ve 5’i çarpıp 1 ekleyip ikiye bölelim. $$ \frac{3 \cdot 5 + 1}{2} = 8 $$ $$ 8 - 2 = 6 $$ Bunun normal bir şekilde yapmaktan daha uzun sürebileceğinin farkındayım, ancak bu büyük ve hesaplaması uzun sayılar için kullanması mantıklı olan bir seçenek, örneğin 30’un 12 tane böyle çifti var. Bu soruları gerçekten çok hızlı çözmek istiyorsanız baştan başlayarak hesaplamak yerine bazı başlangıç noktalarını ezberleyerek oradan başlayabilirsiniz birkaç tanesini vereyim:
| x | f(x) |
|---|---|
| 5 | 1 |
| 10 | 10 |
| 15 | 22 |
| 20 | 37 |
İstediğiniz kadarını programımı kullanarak bulabilirsiniz: https://github.com/Terracotta-Lite/lcm-pairs